学习笔记

如果在一个平面上给我们若干个图形求面积并，这一看就是个计算几何问题，感觉不太能用数据结构来维护，但是当这些图形都是矩形，那么问题就变的简单了，为什么，因为一旦是一堆矩形，那么对于这些相交的矩形，我们是可以将其分成若干的块的。这里为了更加形象化的理解，就借用 $oi-wiki$ 上的图来帮助理解一下。

如图所示，这一整块矩形的集合被重新分成了若干块规则的矩形，但我们知道了其具体的坐标的时候，我们会发现我们想要维护矩形的底是非常好维护的，那么除了底，我们就只需要维护一下高即可。

那么为了解决这种问题，我们是可以将这个红线引入到代码中，这个红线就是我们所说的扫描线，当我们处理这个矩形的时候考虑一个矩形的下底造成的贡献的是一直到了他的上底，我们不妨将一个矩形给拆成两条有距离的线段，下底为 $+1$ ，上底为 $-1$ ，此外我们可以记录一个 $y$ 表示当前线段所在的纵坐标。那么扔到一个结构体里就是这样。

	struct Line
	{
	int x1, x2; // 线段的左右端点
	int y; // 纵坐标

	bool operator < (const Line &a) const {return y < a.y;} // 重载小于符号
	} line[N];

那么我们现在就只需将上面的那个线排序后再挨个进行线段树的区间修改即可。那么我们来看下模板题。

# 扫描线

# 题目描述

求 $n$ 个四边平行于坐标轴的矩形的面积并。

# 输入格式

第一行一个正整数 $n$ 。

接下来 $n$ 行每行四个非负整数 $x_1, y_1, x_2, y_2$ ，表示一个矩形的四个端点坐标为 $(x_1, y_1),(x_1, y_2),(x_2, y_2),(x_2, y_1)$ 。

# 输出格式

一行一个正整数，表示 $n$ 个矩形的并集覆盖的总面积。

# 提示

对于 $20\%$ 的数据， $1 \le n \le 1000$ 。
对于 $100\%$ 的数据， $1 \le n \le {10}^5$ ， $0 \le x_1 < x_2 \le {10}^9$ ， $0 \le y_1 < y_2 \le {10}^9$ 。

# 分析

我们这里先重点看一下数据范围，对于这道题来说，他的横坐标很大，纵坐标很大，但是矩形数量很少，那么我们会很自然的想到对坐标进行离散化。但是在离散化的时候就会出些问题，我们看下面一组数据。

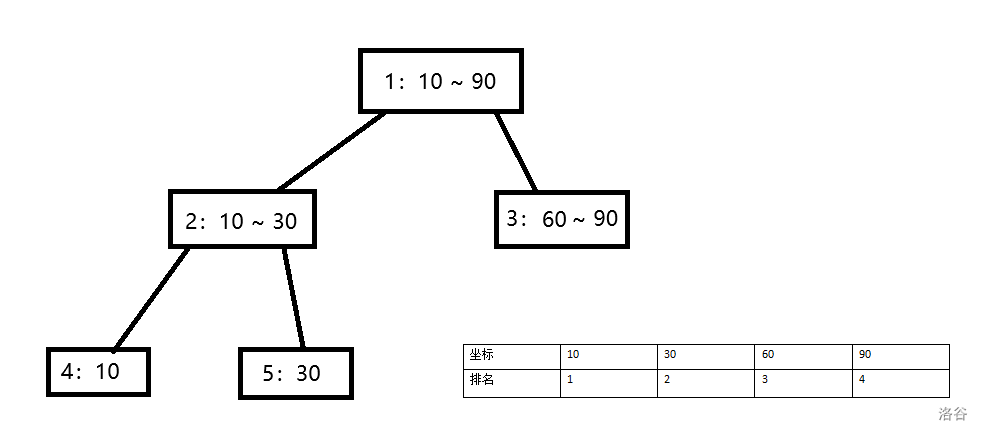
在这个线段树中我们虽然是分成左右儿子分别处理，但是我们会发现二号节点和三号节点的左右端点是不相连的，但是在图上这可能是相连的，那么我们为了让坐标连续起来，我们可以对所有节点的右儿子进行一个向右的偏移，那么偏移后我们就会发现此时左右子树连续起来了，但是我们左右节点分别掌管的区域还是偏移前的，因此在进行修改操作的时候要再把偏移量减回来。然后剩下的就是最基本的线段树的操作了，具体细节可以看代码。

	#include <cstring>
	#include <iostream>
	#include <algorithm>

	namespace read_write
	{
	template <typename T>
	inline void read(T &x)
	{
	x = 0;
	T f = 1;
	char ch = getchar();
	while (ch > '9' \|\| ch < '0')
	{
	if (ch == '-')
	f = -1;
	ch = getchar();
	}
	while (ch >= '0' && ch <= '9')
	x = x * 10 + ch - '0', ch = getchar();
	x *= f;
	return;
	}

	template <typename T>
	inline void write(T x)
	{
	if (x < 0)
	{
	x = -x;
	putchar('-');
	}
	if (x > 9)
	write(x / 10);
	putchar(x % 10 + '0');
	}

	template <typename T>
	T max(T x, T y)
	{
	return x > y ? x : y;
	}

	template <typename T>
	T min(T x, T y)
	{
	return x > y ? y : x;
	}

	template <typename T>
	void swap(T &a, T &b)
	{
	T tem = b;
	b = a;
	a = tem;
	}
	}

	namespace Segment_Tree
	{
	using namespace read_write;

	#define int long long

	const int N = 1e6 + 10;

	int n, ans;
	int X[N];

	struct Line
	{
	int x1, x2, y;
	int tag;

	bool operator < (const Line &a) const {return y < a.y;}
	} line[N];

	struct Tree
	{
	int l, r, cnt, len;
	} tr[N << 1];

	void pushup(int u)
	{
	int l = tr[u].l, r = tr[u].r;
	if(tr[u].cnt) // 对于区间是连续的直接用右端点减去左端点
	tr[u].len = X[r + 1] - X[l];
	else // 不连续的我们则将左右儿子的长度进行加和
	tr[u].len = tr[u << 1].len + tr[u << 1 \| 1].len;
	}

	void modify(int u, int l, int r, int tag)
	{
	if(l <= tr[u].l && r >= tr[u].r)
	{
	tr[u].cnt += tag;
	pushup(u);
	return ;
	}
	int mid = tr[u].l + tr[u].r >> 1;
	if(l <= mid)
	modify(u << 1, l, r, tag);
	if(r > mid)
	modify(u << 1 \| 1, l, r, tag);
	pushup(u);
	}

	void build(int u, int l, int r)
	{
	tr[u].l = l, tr[u].r = r;
	if(l == r)
	return ;
	int mid = l + r >> 1;
	build(u << 1, l, mid), build(u << 1 \| 1, mid + 1, r);
	}
	}

	namespace Solve
	{
	using namespace Segment_Tree;

	void solve()
	{
	read(n);

	for(int i = 1 ; i <= n ; ++ i)
	{
	int X1, X2, Y1, Y2;
	read(X1), read(Y1), read(X2), read(Y2);
	line[i] = {X1, X2, Y1, 1}; // 下底
	line[i + n] = {X1, X2, Y2, -1}; // 上底
	X[i] = X1, X[n + i] = X2; // 将点扔进用于离散化的数组中
	}

	n <<= 1;
	std :: sort(line + 1, line + n + 1);
	std :: sort(X + 1, X + n + 1);
	int Uni = std :: unique(X + 1, X + n + 1) - X - 1; // 去重
	build(1, 1, Uni - 1);

	for(int i = 1 ; i < n ; ++ i)
	{
	int l = std :: lower_bound(X + 1, X + Uni + 1, line[i].x1) - X;
	int r = std :: lower_bound(X + 1, X + Uni + 1, line[i].x2) - X;
	modify(1, l, r - 1, line[i].tag); // 记得我们是偏移过右坐标了
	ans += tr[1].len * (line[i + 1].y - line[i].y);
	}

	write(ans);
	}
	}

	signed main()
	{
	Solve :: solve();

	return 0;
	}

# 最后还有一道例题

数据结构笔记线段树