首页 学习笔记 期望

做笔试题发现自己期望这块太烂了于是就做了一晚上的期望题

# 六省联考 2017 分手是祝愿

# 题目描述

Zeit und Raum trennen dich und mich.
时空将你我分开。

B 君在玩一个游戏，这个游戏由 nn 个灯和 nn 个开关组成，给定这 nn 个灯的初始状态，下标为从 11 到 nn 的正整数。

每个灯有两个状态亮和灭，我们用 11 来表示这个灯是亮的，用 00 表示这个灯是灭的，游戏的目标是使所有灯都灭掉。

但是当操作第 ii 个开关时，所有编号为 ii 的约数（包括 11 和 ii）的灯的状态都会被改变，即从亮变成灭，或者是从灭变成亮。

B 君发现这个游戏很难，于是想到了这样的一个策略，每次等概率随机操作一个开关，直到所有灯都灭掉。

这个策略需要的操作次数很多，B 君想到这样的一个优化。如果当前局面，可以通过操作小于等于 kk 个开关使所有灯都灭掉，那么他将不再随机，直接选择操作次数最小的操作方法（这个策略显然小于等于 kk 步）操作这些开关。

B 君想知道按照这个策略（也就是先随机操作，最后小于等于 kk 步，使用操作次数最小的操作方法）的操作次数的期望。

这个期望可能很大，但是 B 君发现这个期望乘以 nn 的阶乘一定是整数，所以他只需要知道这个整数对 100003100003 取模之后的结果。

# 分析

首先看题发现我们对于这个灯的控制是能控制所有约数的位置，那么这就会有一个很好的性质即你改变任意一个灯的状态实际上会改变状态的就只有他之前的灯，也就是说小的灯是影响不到大的灯，因此对于最优状态，我们一定是从后往前去挨个更新一定是最优的，那么到这里，就可以拿到 80 分了，我们考虑怎么去求随机的那部分。

我们设 f[i]f[i] 表示当前有 ii 盏灯是亮着的，那么我们的状态转移就是

f[i]=inf[i−1]+n−inf[i+1]+1f[i] = \frac{i}{n} f[i - 1] + \frac{n - i}{n}f[i + 1] + 1

然后对于这个式子接着进行化简，首先 f[n]=f[n−1]+1f[n] = f[n - 1] + 1 ，我们接着化简最后会发现 f[i]=f[i−1]+gif[i] = f[i - 1] + g_i ，其中 gig_i 为常量，那么我们再带入进一步化简会发现 gi=(n−i)g[i+1]+nig_i = \frac{(n - i)g[i + 1] + n}{i} ，g[n]=1g[n] = 1 ，然后带入算即可。

#include <cmath>
#include <cstring>
#include <iostream>
#include <algorithm>
namespace read_write
{
    template <typename T>
    inline void read(T &x)
    {
        x = 0;
        T f = 1;
        char ch = getchar();
        while (ch > '9' || ch < '0')
        {
            if (ch == '-')
                f = -1;
            ch = getchar();
        }
        while (ch >= '0' && ch <= '9')
            x = x * 10 + ch - '0', ch = getchar();
        x *= f;
        return;
    }
    template <typename T>
    inline void write(T x)
    {
        if (x < 0)
        {
            x = -x;
            putchar('-');
        }
        if (x > 9)
            write(x / 10);
        putchar(x % 10 + '0');
    }
    template <typename T>
    T max(T x, T y)
    {
        return x > y ? x : y;
    }
    template <typename T>
    T min(T x, T y)
    {
        return x > y ? y : x;
    }
    template <typename T>
    void swap(T &a, T &b)
    {
        T tem = b;
        b = a;
        a = tem;
    }
}
namespace Solve
{
    using namespace read_write;
    #define int long long
    const int N = 1e6 + 10, mod = 100003;
    int n, k;
    int w[N], g[N], f[N];
    int fac = 1, cnt;
    int infac[N];
    int qmi(int a, int k)
    {
        int res = 1;
        while(k)
        {
            if(k & 1)
                res = res * a % mod;
            a = a * a % mod;
            k >>= 1;
        }
        return res;
    }
    void solve()
    {
        read(n), read(k);
        g[n] = 1, f[k] = k;
        for(int i = 1 ; i <= n ; ++ i)
            read(w[i]), fac = fac * i % mod;
        for(int i = n ; i >= 1 ; -- i)
        {
            if(w[i])
            {
                cnt ++ ;
                for(int j = 1 ; j * j <= i ; ++ j)
                {
                    if(i % j == 0)
                    {
                        w[j] ^= 1;
                        if(j * j != i)
                            w[i / j] ^= 1;
                    }
                }
            }
        }
        if(cnt <= k)
        {
            write((cnt * fac) % mod);
            exit(0);
        }
        for(int i = n - 1 ; i > k ; -- i)
            g[i] = ((n - i) * g[i + 1] % mod + n)  % mod * qmi(i, mod - 2) % mod; 
        for(int i = k + 1 ; i <= cnt ; ++ i)
            f[i] = (f[i - 1] + g[i]) % mod;
        write(f[cnt] * fac % mod);
    }
}
signed main()
{
    Solve :: solve();
    return 0;
}
# SHOI2012 随机树
# 题目描述
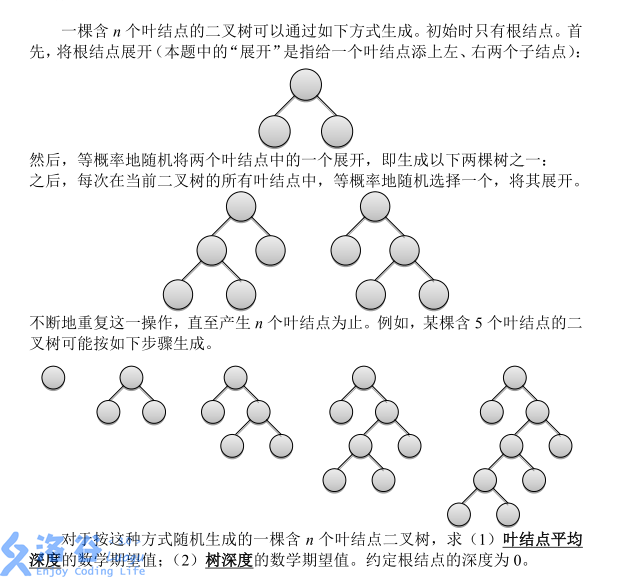
# 分析
对于这个题，首先我们考虑第一问，这个还是比较好处理的，我们新加入一个节点，设之前的平均深度为 xx ，那么我们加入之后是新加了两个单位的深度，那么我们将其分摊到所有点上即为贡献。然后考虑第二问，我们设 f[i][j]f[i][j] 为 ii 个节点的树，深度为 jj 的概率，那么 ans=∑i=0ni×f[n][i]ans = \sum_{i = 0}^{n} i \times f[n][i] ，那么我们的转移即为
f[i][j]=∑l=1i−1p[i][l]∑x=1j∑y=1jf[l][x]∗f[i−l][y]f[i][j] = \sum_{l = 1}^{i - 1} p[i][l] \sum_{x = 1}^{j} \sum_{y = 1}^{j} f[l][x] * f[i - l][y]
p[i][j]p[i][j] 为有 ii 个节点的树，左边有 jj 个点的概率，这个转移的复杂度很高，打达到了 O(n4)O(n^4) ，接着考虑优化，设 g[i][j]=∑i=1jf[i][j]g[i][j] = \sum_{i = 1}{j}f[i][j]
然后式子就变成了
f[i][j]=∑l=1i−1×(2×f[l][j−1]×g[i−l][j−1]−f[l][j−1]×f[i−l][j−1])f[i][j] = \sum_{l = 1}^{i - 1} \times (2 \times f[l][j - 1] \times g[i - l][j - 1] - f[l][j - 1] \times f[i - l][j - 1])
然后就递推求即可
#include <cstring>
#include <iostream>
#include <algorithm>
namespace read_write
{
    template <typename T>
    inline void read(T &x)
    {
        x = 0;
        T f = 1;
        char ch = getchar();
        while (ch > '9' || ch < '0')
        {
            if (ch == '-')
                f = -1;
            ch = getchar();
        }
        while (ch >= '0' && ch <= '9')
            x = x * 10 + ch - '0', ch = getchar();
        x *= f;
        return;
    }
    template <typename T>
    inline void write(T x)
    {
        if (x < 0)
        {
            x = -x;
            putchar('-');
        }
        if (x > 9)
            write(x / 10);
        putchar(x % 10 + '0');
    }
    template <typename T>
    T max(T x, T y)
    {
        return x > y ? x : y;
    }
    template <typename T>
    T min(T x, T y)
    {
        return x > y ? y : x;
    }
    template <typename T>
    void swap(T &a, T &b)
    {
        T tem = b;
        b = a;
        a = tem;
    }
}
namespace Solve
{
    const int N = 1e3 + 10;
    int n, q;
    double f[N][N], g[N][N], ans;
    void solve()
    {
        read_write :: read(q), read_write :: read(n);
        
        if(q == 1)
        {
            for(int i = 2 ; i <= n ; ++ i)
                ans += 2.0 / i;
            printf("%lf", ans);
        }
        else 
        {
            f[1][0] = 1;
            for(int i = 0 ; i <= n ; ++ i)
                g[1][i] = 1;
            for(int i = 2 ; i <= n ; ++ i)
            {
                for(int s = 0 ; s < i ; ++ s)
                    for(int l = 1 ; l < i ; ++ l)
                        f[i][s + 1] = f[i][s + 1] + (2 * f[l][s] * g[i - l][s] - f[l][s] * f[i - l][s]) / (i - 1);
                g[i][0] = f[i][0];
                for(int s = 1 ; s <= n ; ++ s)
                    g[i][s] = g[i][s - 1] + f[i][s];
            }
            for(int i = 1 ; i <= n ; ++ i)
                ans += i * f[n][i];
            printf("%lf", ans);
        }
    }
}
int main()
{
    Solve :: solve();
    return 0;
}
# SCOI2008 奖励关
# 题目描述
你正在玩你最喜欢的电子游戏，并且刚刚进入一个奖励关。在这个奖励关里，系统将依次随机抛出 kk 次宝物，每次你都可以选择吃或者不吃（必须在抛出下一个宝物之前做出选择，且现在决定不吃的宝物以后也不能再吃）。
宝物一共有 nn 种，系统每次抛出这 nn 种宝物的概率都相同且相互独立。也就是说，即使前 (k−1)(k-1) 次系统都抛出宝物 11（这种情况是有可能出现的，尽管概率非常小），第 kk 次抛出各个宝物的概率依然均为 $\frac 1 n $。
获取第 ii 种宝物将得到 pip_i 分，但并不是每种宝物都是可以随意获取的。第 ii 种宝物有一个前提宝物集合 sis_i。只有当 sis_i 中所有宝物都至少吃过一次，才能吃第 ii 种宝物（如果系统抛出了一个目前不能吃的宝物，相当于白白的损失了一次机会）。注意，pip_i 可以是负数，但如果它是很多高分宝物的前提，损失短期利益而吃掉这个负分宝物将获得更大的长期利益。
假设你采取最优策略，平均情况你一共能在奖励关得到多少分值？
# 分析
对于这种集合类的题，我们首先是考虑把集合压成二进制，然后我们设 f[i][j]f[i][j] 表示到了第 ii 轮，当前状态是 jj ，那么转移就是
f[i][j]={f[i+1][j∣(1<<(zt[k]−1))]+s[k](j&zt[i]==zt[k])f[i+1][j]f[i][j] = \begin{cases} f[i + 1][j \; | \; (1 << (zt[k] - 1))] + s[k] \quad (j \; \& \; zt[i] == zt[k]) \\ f[i + 1][j] \end{cases}
#include <cstring>
#include <iostream>
#include <algorithm>
namespace read_write
{
    template <typename T>
    inline void read(T &x)
    {
        x = 0;
        T f = 1;
        char ch = getchar();
        while (ch > '9' || ch < '0')
        {
            if (ch == '-')
                f = -1;
            ch = getchar();
        }
        while (ch >= '0' && ch <= '9')
            x = x * 10 + ch - '0', ch = getchar();
        x *= f;
        return;
    }
    template <typename T>
    inline void write(T x)
    {
        if (x < 0)
        {
            x = -x;
            putchar('-');
        }
        if (x > 9)
            write(x / 10);
        putchar(x % 10 + '0');
    }
    template <typename T>
    T max(T x, T y)
    {
        return x > y ? x : y;
    }
    template <typename T>
    T min(T x, T y)
    {
        return x > y ? y : x;
    }
    template <typename T>
    void swap(T &a, T &b)
    {
        T tem = b;
        b = a;
        a = tem;
    }
}
namespace Solve
{
    using namespace read_write;
    const int N = 100 + 10;
    int n, k;
    int s[N], zt[N];
    double f[N][1 << 16];
    void solve()
    {
        read(k), read(n);
        for(int i = 1 ; i <= n ; ++ i)
        {
            int x;
            read(s[i]), read(x);
            while(x)
                zt[i] = zt[i] | (1 << (x - 1)), read(x);
        }
        for(int i = k ; i >= 1 ; -- i)
        {
            for(int j = 0 ; j < (1 << n) ; ++ j)
            {
                for(int zl = 1 ; zl <= n ; ++ zl)
                {
                    if((j & zt[zl]) == zt[zl])
                        f[i][j] += max(f[i + 1][j], f[i + 1][j | (1 << (zl - 1))] + s[zl]);
                    else 
                        f[i][j] += f[i + 1][j];    
                }
                f[i][j] /= n;
            }
        }
        printf("%.6lf", f[1][0]);
    }
}
int main()
{
    Solve :: solve();
    return 0;
}
# [HNOI2015 亚瑟王]
# 题目描述
小 K 不慎被 LL 邪教洗脑了，洗脑程度深到他甚至想要从亚瑟王邪教中脱坑。他决定，在脱坑之前，最后再来打一盘亚瑟王。既然是最后一战，就一定要打得漂亮。众所周知，亚瑟王是一个看脸的游戏，技能的发动都是看概率的。
作为一个非洲人，同时作为一个前 OIer，小 K 自然是希望最大化造成伤害的期望值。但他已经多年没写过代码，连 Spaly 都敲不对了，因此，希望你能帮帮小 K，让他感受一下当欧洲人是怎样的体验。
本题中我们将考虑游戏的一个简化版模型。 玩家有一套卡牌，共 nn 张。游戏时，玩家将 nn 张卡牌排列成某种顺序，排列后将卡牌按从前往后依次编号为 1−n1 - n。本题中，顺序已经确定，即为输入的顺序。每张卡牌都有一个技能。第 ii 张卡牌的技能发动概率为 pip_i，如果成功发动，则会对敌方造成 did_i 点伤害。也只有通过发动技能，卡牌才能对敌方造成伤害。基于现实因素以及小 K 非洲血统的考虑，pip_i 不会为 00，也不会为 11，即 0<pi<10 < p_i < 1。 一局游戏一共有 rr 轮。在每一轮中，系统将从第一张卡牌开始，按照顺序依次考虑每张卡牌。在一轮中，对于依次考虑的每一张卡牌：
  1. 如果这张卡牌在这一局游戏中已经发动过技能，则
1.1. 如果这张卡牌不是最后一张，则跳过之（考虑下一张卡牌）； 否则（是最后一张），结束这一轮游戏。
  1. 否则（这张卡牌在这一局游戏中没有发动过技能），设这张卡牌为第 ii 张
2.1. 将其以 pip_i 的概率发动技能。
2.2. 如果技能发动，则对敌方造成 did_i 点伤害，并结束这一轮。
2.3. 如果这张卡牌已经是最后一张（即 ii 等于 nn），则结束这一轮；否则，考虑下一张卡牌。
请帮助小 K 求出这一套卡牌在一局游戏中能造成的伤害的期望值。
# 分析
这个一开始不是特别好想，然后我们再分析一下题意会发现每张卡的贡献是独立的，而且我们最终的贡献即为每张卡的发动的概率乘上他的伤害，那么我们就可以设 f[i][j]f[i][j] 为前 ii 张卡中选出了 jj 张卡的概率，那么我们考虑第 ii 张卡选还是不选，不选的话就是 f[i][j]+=f[i−1][j]×ir−jf[i][j] += f[i - 1][j] \times i^{r - j} ，选即为 f[i][j]+=f[i−1][j−1]∗(1−ir−j+1)f[i][j] += f[i - 1][j - 1] * (1 - i^{r - j + 1}) ，那么每张卡 的触发概率 p=f[i−1][j]∗(1−ir−jp = f[i - 1][j] * (1 - i^{r - j} 。
#include <cstring>
#include <iostream>
#include <algorithm>
namespace read_write
{
    template <typename T>
    inline void read(T &x)
    {
        x = 0;
        T f = 1;
        char ch = getchar();
        while (ch > '9' || ch < '0')
        {
            if (ch == '-')
                f = -1;
            ch = getchar();
        }
        while (ch >= '0' && ch <= '9')
            x = x * 10 + ch - '0', ch = getchar();
        x *= f;
        return;
    }
    template <typename T>
    inline void write(T x)
    {
        if (x < 0)
        {
            x = -x;
            putchar('-');
        }
        if (x > 9)
            write(x / 10);
        putchar(x % 10 + '0');
    }
    template <typename T>
    T max(T x, T y)
    {
        return x > y ? x : y;
    }
    template <typename T>
    T min(T x, T y)
    {
        return x > y ? y : x;
    }
    template <typename T>
    void swap(T &a, T &b)
    {
        T tem = b;
        b = a;
        a = tem;
    }
}
namespace Solve
{
    using namespace read_write;
    const int N = 400 + 10;
    int n, t, r, d[N]; 
    double p[N], f[N][N];    //f [i][j] : 前 i 张卡中选出了 j 张卡的概率
    double Pow[N][N], use[N], ans;
    void init()
    {
        for(int i = 0 ; i < n ; ++ i)
        {
            Pow[i][0] = 1;
            for(int j = 1 ; j <= r ; ++ j)
                Pow[i][j] = Pow[i][j - 1] * (1 - p[i]);
        }
    }
    void solve()
    {
        read(t);
        while(t --)
        {
            read(n), read(r);
            for(int i = 0 ; i < n ; ++ i)
            {
                scanf("%lf", &p[i]);
                read(d[i]);
            }
            init(), ans = 0;
            memset(f, 0, sizeof(f));
            memset(use, 0, sizeof(use));
            f[0][0] = Pow[0][r];
            f[0][1] = use[0] = 1 - f[0][0];
            for(int i = 1 ; i < n ; ++ i)
            {
                for(int j = 0 ; j <= r ; ++ j)
                {
                    use[i] += f[i - 1][j] * (1 - Pow[i][r - j]);   
                    f[i][j] += f[i - 1][j] * Pow[i][r - j];   // 不选
                    if(j)
                        f[i][j] += f[i - 1][j - 1] * (1 - Pow[i][r - j + 1]);  // 选
                }
            }
            for(int i = 0 ; i < n ; ++ i)
                ans += d[i] * use[i];
            printf("%.10lf", ans), puts("");
        }
    }
}
int main()
{
    Solve :: solve();
    return 0;
}
以后应该会接着更新吧，总之先咕。
 
 更新于   阅读次数  次
请我喝[茶]~(￣▽￣)~*
Tokai Teio 微信支付
微信支付
Tokai Teio 支付宝
支付宝
Tokai Teio 贝宝
贝宝