首页 笔记 动态规划

学习笔记

# 斜率优化 dp 阉割版（都单调的情况）

在一上午的 jzp 学长的传授后，最终还是稍微理解了什么是斜率优化 dp。(有一说一，这玩意是真抽象，提前看了看别人写的博客还是不太理解)

首先如果我们要考虑怎么用斜率优化 dp ，得先知道这里的斜率指的是什么，我当我们没有学的时候，我们凭借对一次函数的认识可以感性的认为斜率指的是 y=kx+by = kx + b 中的 kk 值，而实际上我们这里的斜率和一次函数的斜率还是非常的相似（个人感觉就是一样的）。

我们先看一下这道题

# [HNOI2008] 玩具装箱

# 题目描述

P 教授有编号为 1⋯n1 \cdots n 的 nn 件玩具，第 ii 件玩具经过压缩后的一维长度为 CiC_i。

为了方便整理，P 教授要求：

  • 在一个一维容器中的玩具编号是连续的。

  • 同时如果一个一维容器中有多个玩具，那么两件玩具之间要加入一个单位长度的填充物。形式地说，如果将第 ii 件玩具到第 jj 个玩具放到一个容器中，那么容器的长度将为 x=j−i+∑k=ijCkx=j-i+\sum\limits_{k=i}^{j}C_k。

制作容器的费用与容器的长度有关，根据教授研究，如果容器长度为 xx，其制作费用为 (x−L)2(x-L)^2。其中 LL 是一个常量。P 教授不关心容器的数目，他可以制作出任意长度的容器，甚至超过 LL。但他希望所有容器的总费用最小。

# 分析：

对于这道题我们如果不看数据范围，可能很容易就写出一个比较简单的状态转移方程，我们先设 s[i]=∑j=1ic[j]+1s[i] = \sum_{j = 1}^ic[j] + 1， 然后我们的转移方程就变成了 ： dp[i]=min(dp[j]+(s[i]−s[j]−L−1)2)(j<i)dp[i] = min(dp[j] + (s[i] - s[j] - L - 1)^2) (j < i) 。显然这个转移方程的复杂度是这个题的数据范围难以忍受的。然后我们考虑怎么优化。

我们稍微想一下就会发现，其实我们在上面的转移中会有许多的冗余步骤，因为对于一个状态的转移，这个状态的有效转移的上一个状态的个数实际上是远小于我们所暴力枚举的这个区间的的，你会发现是不是跟当初单调队列优化的时候所出现的问题差不多，既然出现的问题差不多，我们是不是可以考虑一下是不是可以用类似的方法去解决这道题呢？

首先我们对于上面的式子进行拆分。我们可以先把 minmin 给拆掉，就变成了 dp[i]=dp[j]+(s[i]−s[j]−L−1)2dp[i] = dp[j] + (s[i] - s[j] - L - 1) ^ 2。然后，我们再把平方拆开，就变成了 dp[i]=s[i]2−2s[i]L+dp[j]+(s[j]+L)2−2s[i]s[j]dp[i] = s[i] ^ 2 - 2s[i]L + dp[j] + (s[j] + L)^2 - 2s[i]s[j] ，我们假定我们现在有两个状态，分别是 j1j_1 和 j2j_2。我们考虑当 j1j_1 < j2j_2 时，需要满足什么条件。

我们可以对式子进行划分 (这里为了方便就直接借用辰星凌大佬写好的式子了)

然后我们设 X(i)=s[i],Y(i)=dp[i]+(s[i]+L)2X(i) = s[i], Y(i) = dp[i] + (s[i] + L) ^ 2。

我们对其进行移项和化简就能得到 $2s [i] \geq \frac {Y (j_2)-Y (j_1)}{X (j_2)-X (j_1)} $。然后我们就可以得出，如果对于两个状态如果满足这个式子，那么后面的状态是优于前面的这个状态的的，如果我们对于每个相邻点，只保留后面的点优于前面的点的一系列的点，实际上就是一个单调递增的一堆点，如果我们在这里将更优的这个性质转换成斜率的话，因为是单调递增，所以最终就构成了一个下凸壳。

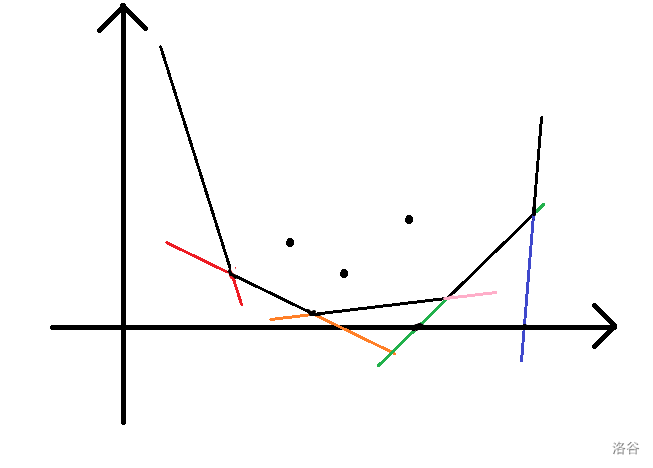
每条彩线是每个节点对应的斜率也就是上面花间之后的那个值，中间的黑点为什么没有选择，主要是因为当我们选择他们之后会让答案变的更劣，所以我们最终维护的就是一个下凸壳。

那么我们最终对状态转移的时候只需每次选取凸壳上的点进行转移即可，而维护凸壳的方法有很多，比如单调队列，单调栈，CDQ，平衡树等等，这里我用的是单调队列，因为相对比较好写和好调，但是会有特殊情况。（因为这道题里的 x 和 最后转换之后的式子是单调的，所以我们可以直接维护一个凸壳，但是有的时候是不单调的，那么我们就只能通过其他方式去维护了，其中受限制最小的李超线段树，理论上是任何情况下通用的）

下面是代码实现

#include <cstring>
#include <iostream>
#include <algorithm>
#define int long long
namespace read_write
{
    template <typename T>
    inline void read(T &x)
    {
        x = 0;
        T f = 1;
        char ch = getchar();
        while (ch > '9' || ch < '0')
        {
            if (ch == '-')
                f = -1;
            ch = getchar();
        }
            while (ch >= '0' && ch <= '9')
                x = x * 10 + ch - '0', ch = getchar();
        x *= f;
        return;
    }
    template <typename T>
    inline void write(T x)
    {
        if (x < 0)
        {
            x = -x;
            putchar('-');
        }
        if (x > 9)
            write(x / 10);
        putchar(x % 10 + '0');
    }
    template <typename T>
    T max(T x, T y)
    {
        return x > y ? x : y;
    }
    template <typename T>
    T min(T x, T y)
    {
        return x > y ? y : x;
    }
    template <typename T>
    void swap(T &a, T &b)
    {
        T tem = b;
        b = a;
        a = tem;
    }
}
namespace Solve
{
    using namespace read_write;
    const int N = 1e6 + 10;
    int n, L;
    int w[N], q[N], hh = 1, tt;
    int s[N], dp[N];   //:s[i] = c[k] + 1  (1 <= k <= i)
    int calc_Y(int x)
    {
        return dp[x] + (s[x] + L) * (s[x] + L); 
    }
    int calc_X(int x)
    {
        return s[x];
    }
    double calc(int x, int y)
    {
        return (double) ((calc_Y(y) - calc_Y(x)) / (calc_X(y) - calc_X(x)));
    }
    void solve()
    {
        read(n), read(L);
        ++ L;
        for(int i = 1 ; i <= n ; ++ i)
        {
            read(w[i]);
            s[i] = s[i - 1] + w[i] + 1;
        }
        //for(int i = 1 ; i <= n ; ++ i)
        //    write(s[i]), putchar(' ');
        q[++ tt] = 0;
        for(int i = 1 ; i <= n ; ++ i)
        {   
            while(hh < tt && calc(q[hh], q[hh + 1]) <= 2 * s[i])
                hh ++;
            int fron = q[hh];
            dp[i] = dp[fron] + (s[i] - s[fron] - L) * (s[i] - s[fron] - L);
            while(hh < tt && calc(q[tt - 1], q[tt]) >= calc(q[tt - 1], i))
                tt --;
            q[++ tt] = i;
        }
        write(dp[n]);
    }
}
signed main()
{
    Solve::solve();
    return 0;
}
# Cats Transport
# 题面翻译
Zxr960115 是一个大农场主。
他养了 mm 只可爱的猫子，雇佣了 pp 个铲屎官。这里有一条又直又长的道路穿过了农场，有 nn 个山丘坐落在道路周围，编号自左往右从 11 到 nn。山丘 ii 与山丘 i−1i-1 的距离是 DiD_i 米。铲屎官们住在 11 号山丘。
一天，猫子们外出玩耍。猫子 ii 去山丘 HiH_i 游玩，在 TiT_i 时间结束他的游玩，然后在山丘 HiH_i 傻等铲屎官。铲屎官们必须把所有的猫子带上。每个铲屎官直接从 H1H_1 走到 HnH_n，中间不停下，可以认为不花费时间的把游玩结束的猫子带上。每个铲屎官的速度为一米每单位时间，并且足够强壮来带上任意数量的猫子。
举个栗子，假装我们有两个山丘 ( D2=1D_2=1 )，有一只猫子，他想去山丘 22 玩到时间 33。然后铲屎官如果在时间 22 或者时间 33 从 11 号山丘出发，他就能抱走猫子。如果他在时间 11 出发那么就不行 (猫子还在玩耍)。如果铲屎官在时间 22 出发，猫子就不用等他（ΔT=0\Delta T=0）。如果他在时间 33 出发，猫子就要等他 11 个单位时间。
你的任务是安排每个铲屎官出发的时间 (可以从 0 时刻之前出发），最小化猫子们等待的时间之和。
# 分析：
这道题也非常的经典，一开始的状态转移也比较好写，我们先将题中的数据转换一下，我们考虑对于每一个猫来说，你最早的出发时间就是那个那座山里第一座山的距离再减去猫游玩的时间（因为这里的速度是 1m/s），我们先记这个时间为 a[i]a[i] ，然后我们就可以设 f[i][j]f[i][j] 为派出了 ii 个人，已经接了 jj 只猫，猫所等待的时间，然后转移式子就是
# f[i][j]=min(f[i−1][k]+a[j]∗(j−k)−∑l=k+1ja[l])f[i][j] = min(f[i - 1][k] + a[j] * (j - k) - \sum_{l = k + 1}^{j}a[l])
这个式子实际上就是从 f[i][k]f[i][k] 这个式子转移过来的，然后多的时间就是在 k+1k + 1 到 jj 之前的猫全按照不玩，等了 a[j]a[j] 的时间，最后再减去每只猫本身出发的时间。
对于这个 a[i]a[i] 数组我们其实可以通过预处理前缀和来优化一下，这里我们计 sum[i]=∑j=1ia[i]sum[i] = \sum_{j = 1}^i a[i] ，然后我们上面的那个式子就变成了
# f[i][j]=min(f[i−1][k]+a[j]∗(j−k)−(sum[j]−sum[k]))f[i][j] = min(f[i - 1][k] + a[j] * (j - k) - (sum[j] - sum[k]))
然后我们会发现只有 kk 是一只在变化的， ii 和 jj 都是枚举的，固定不变的，我们就可以考虑把 kk 给单独提出来，这里我们再设 w(k,i)=f[i−1][k]+sum(k)w(k, i) = f[i - 1][k] + sum(k) ，这样我们的式子就进一步的转换为
# f[i][j]=min(w(i,j)+a[j]∗(j−k)−sum[j])f[i][j] = min(w(i,j) + a[j]*(j - k) -sum[j])
然后我们可以考虑将 minmin 先去掉，因为我们肯定是要去找最小值的，我们考虑在什么情况下，后面的状态会比前面的状态更优，我们设 k1k_1 和 k2k_2，当由 k1k_1 转移过来的状态比由 k2k_2 转移过来的状态更优时，因为要找最小值，且此时 jj 的值是固定的，因此我们就可以把只含 jj 的那项给删掉，然后就会得到一个不等式
# w(k1,j)+a[j]∗(j−k1)≤w(k2,j)+a[j]∗(j−k2)w(k_1,j) + a[j]*(j - k_1) \leq w(k_2,j) + a[j]*(j - k_2)
然后再移项
# w(k1,j)−w(k2,j)≤a[j]∗(k1−k2)w(k_1, j) - w(k_2, j) \leq a[j]*(k_1-k_2)
最后我们想要去维护，肯定需要一个定值，我们就可以让一边只剩下 a[j]a[j]，那么最后就变成了
# w(k2,j)−w(k1,j)k2−k1≤a[j]\frac{w(k_2,j) - w(k_1,j)}{k_2-k_1} \leq a[j]
这里为了方便就将 k1k_1 和 k2k_2 换了一下位置，我们观察最终的这个式子就成只要满足上面的式子那么 k2k_2 就一定是比 k1k_1 更优的。（一般是将 w(k,i)w(k,i) 这类的函数叫做斜率式，实际上就是一种对于更优性的判断标准）
我们的最终的递推式子也就变成了
# f[i][j]=w(k,i)−sum[j]+a[j]∗(j−k)f[i][j] = w(k, i) - sum[j] + a[j]*(j - k)
然后对于上面的状态，因为我们有了更优性的判断的式子，我们就可以通过单调队列来优化更优状态的转移来降低转移复杂度和无用状态。
还有一个比较重要的点就是要将 a[i]a[i] 排序，因为人接猫肯定是接的一整段的连续的时间，所以要将出发时间拍一下序
下面是代码实现（稍微带点比较重要的注释）
#include <cstring>
#include <iostream>
#include <algorithm>
#define int long long
namespace read_write
{
    template <typename T>
    inline void read(T &x)
    {
        x = 0;
        T f = 1;
        char ch = getchar();
        while (ch > '9' || ch < '0')
        {
            if (ch == '-')
                f = -1;
            ch = getchar();
        }
            while (ch >= '0' && ch <= '9')
                x = x * 10 + ch - '0', ch = getchar();
        x *= f;
        return;
    }
    template <typename T>
    inline void write(T x)
    {
        if (x < 0)
        {
            x = -x;
            putchar('-');
        }
        if (x > 9)
            write(x / 10);
        putchar(x % 10 + '0');
    }
    template <typename T>
    T max(T x, T y)
    {
        return x > y ? x : y;
    }
    template <typename T>
    T min(T x, T y)
    {
        return x > y ? y : x;
    }
    template <typename T>
    void swap(T &a, T &b)
    {
        T tem = b;
        b = a;
        a = tem;
    }
}
namespace Solve
{
    using namespace read_write;
    const int N = 2e5 + 10, INF = 1e13 + 10;   //   INF 一定要开的足够大！！！！！！
    int n, p, m;
    int a[N], t[N];
    int f[110][N];   //f [i][j]: 派了 i 个人，接了 j 只猫用的时间
    int q[N], hh, tt;
    int sum[N];
    int calc(int x, int y)   // 就是 w (k,i) 这个式子
    {
        return f[x - 1][y] + sum[y];
    }
    void solve()
    {
        read(n), read(m), read(p);
        for(int i = 2 ; i <= n ; ++ i)   // 预处理距离，一定要处理成前缀和，因为题干中所给的是距离上一座山的距离而不是距离第一座山的距离
        {
            int x;
            read(x);
            t[i] = t[i - 1] + x;
        }
        for(int i = 1 ; i <= m ; ++ i)   // 计算出发时间，顺便初始化 dp 数组
        {
            int x, y;
            read(x), read(y);
            a[i] = y - t[x];
            f[0][i] = INF;
        }
        std::sort(a + 1, a + m + 1);   // 一定要排序
        for(int i = 1 ; i <= m ; ++ i)   // 排完序再处理前缀和，要不然是错的
            sum[i] = a[i] + sum[i - 1];
        for(int i = 1 ; i <= p ; ++ i)
        {
            hh = 1, tt = 0;
            for(int j = 0 ; j <= m ; ++ j)
            {
                while(hh < tt && calc(i, q[hh + 1]) - calc(i, q[hh]) <= a[j] * (q[hh + 1] - q[hh]))   
                    hh ++;   // 如果队头 (hh) 已经小于队头的下一个元素 (hh + 1)，那么队头就没有利用价值，直接弹出就行
                if(hh <= tt)
                    f[i][j] = calc(i, q[hh]) - sum[j] + a[j] * (j - q[hh]);   // 如果当前队列中还有状态，就进行转移
                while(hh < tt && (calc(i, j) - calc(i, q[tt])) * (q[tt] - q[tt - 1]) <= (calc(i, q[tt]) - calc(i, q[tt - 1])) * (j - q[tt]))  
                    tt --;    // 如果队尾的元素不如新插入之后的更优了就要弹出，这里为了避免除法的误差，可以直接乘到对面去
                q[++ tt] = j;   // 将当前元素入队
            }
        }
        write(f[p][m]);
    }
}
signed main()
{
    Solve::solve();
    return 0;
}
# [JSOI2011] 柠檬
# 题目描述
Flute\text{Flute} 很喜欢柠檬。它准备了一串用树枝串起来的贝壳，打算用一种魔法把贝壳变成柠檬。贝壳一共有 nn (1≤n≤100000)(1≤n≤100000) 只，按顺序串在树枝上。为了方便，我们从左到右给贝壳编号 1..n1..n 。每只贝壳的大小不一定相同，贝壳 ii 的大小为 si(1≤si≤10000)s_i(1≤s_i≤10000) 。
变柠檬的魔法要求:Flute:\ \text{Flute} 每次从树枝一端取下一小段连续的贝壳，并选择一种贝壳的大小 s0s_0。如果这一小段贝壳中大小为 s0s_0 的贝壳有 tt 只，那么魔法可以把这一小段贝壳变成 s0t2s_0t^2 只柠檬。Flute\text{Flute} 可以取任意多次贝壳，直到树枝上的贝壳被全部取完。各个小段中，Flute\text{Flute} 选择的贝壳大小 s0s_0 可以不同。而最终 Flute\text{Flute} 得到的柠檬数，就是所有小段柠檬数的总和。
Flute\text{Flute} 想知道，它最多能用这一串贝壳
变出多少柠檬。请你帮忙解决这个问题。
# 分析：
对于这道题我们先不用急着做，我们先看一下是不是有什么性质，首先他说贡献就是你截取的某一段中某种数量的平方和大小的乘积，我们考虑对于选定的一段，要想总贡献最大，我们这一段的头和尾肯定是一样的，因为如果头和尾不一样的话，把尾单独拆出去肯定会比加上尾要更优，然后我们搞清楚了这个小性质就可以开始继续往下搞了。
我们设 f[i]f[i] 为拆到了 ii 的最大贡献，然后我们很快的就能想到去通过一个区间来更新当前状态
f[i]=max(f[j−1]+s[i]∗(ci−cj+1)2)f[i] = max(f[j - 1] + s[i] * (c_i - c_j + 1) ^ 2)
其中 s[j]s[j] 为第 jj 个位置上的该颜色的数量， cic_i 为位置为 ii 的 为颜色是该颜色中第几次出现。这样直接做的时间复杂度是比较难以接受的，我们考虑进一步的将式子进行拆分去看看能不能做进一步的优化，然后可以先将 maxmax 拆掉，然后再将平方拆掉
f[i]=(s[i]∗ci2+2s[i]ci+s[i])+(f[j−1]+s[i]ci2−2s[i]cj)−2s[i]cicjf[i] = (s[i] * c_i^2 + 2s[i]c_i + s[i]) + (f[j - 1] + s[i]c_i^2 - 2s[i]c_j) - 2s[i]c_ic_j
我们将只有 ii，jj 和 i,ji,j 都有的分别括起来然后我们对于只 ii 的，其值是可以确定的，对于含 jj 的，其实际上是单调递增的，所以我们可以直接对其维护一个上凸壳。
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
#define int long long
#define top q[S][q[S].size() - 2]
#define Top q[S][q[S].size() - 1]
namespace read_write
{
    template <typename T>
    inline void read(T &x)
    {
        x = 0;
        T f = 1;
        char ch = getchar();
        while (ch > '9' || ch < '0')
        {
            if (ch == '-')
                f = -1;
            ch = getchar();
        }
        while (ch >= '0' && ch <= '9')
            x = x * 10 + ch - '0', ch = getchar();
        x *= f;
        return;
    }
    template <typename T>
    inline void write(T x)
    {
        if (x < 0)
        {
            x = -x;
            putchar('-');
        }
        if (x > 9)
            write(x / 10);
        putchar(x % 10 + '0');
    }
    template <typename T>
    T max(T x, T y)
    {
        return x > y ? x : y;
    }
    template <typename T>
    T min(T x, T y)
    {
        return x > y ? y : x;
    }
    template <typename T>
    void swap(T &a, T &b)
    {
        T tem = b;
        b = a;
        a = tem;
    }
}
namespace Solve
{
    using namespace read_write;
    const int N = 2e6 + 10;
    int n;
    int f[N], tot[N];
    int last[N], c[N], s[N];
    std::vector<int> q[N];
    int X(int i)
    {
        return c[i];
    }
    int Y(int i)
    {
        return f[i - 1] - 2 * c[i] * s[i] + s[i] * c[i] * c[i];
    }
    double w(int j, int i)
    {
        return 1.0 * (Y(j) - Y(i)) / (X(j) - X(i));
    }
    int calc(int j, int i)
    {
        return f[j - 1] + s[i] * (c[i] - c[j] + 1) * (c[i] - c[j] + 1);
    }
    void solve()
    {
        read(n);
        for (int i = 1; i <= n; ++i)
        {
            read(s[i]);
            c[i] = ++ tot[s[i]];
        }
        for (int i = 1; i <= n; ++i)
        {
            int S = s[i];
            while(q[S].size() >= 2 && w(top, Top) <= w(top, i))
                q[S].pop_back();
            q[S].push_back(i);
            while(q[S].size() >= 2 && calc(Top, i) <= calc(top, i))
                q[S].pop_back();
            f[i] = calc(Top, i);
        }
        write(f[n]);
    }
}
signed main()
{
    Solve::solve();
    return 0;
}
# 最后再说一道例题吧 P2120 [ZJOI2007] 仓库建设
# 题目描述
L 公司有 nn 个工厂，由高到低分布在一座山上，工厂 11 在山顶，工厂 nn 在山脚。
由于地形的不同，在不同工厂建立仓库的费用可能是不同的。第 ii 个工厂目前已有成品 pip_i 件，在第 ii 个工厂位置建立仓库的费用是 cic_i。
对于没有建立仓库的工厂，其产品应被运往其他的仓库进行储藏，而由于 L 公司产品的对外销售处设置在山脚的工厂 nn，故产品只能往山下运（即只能运往编号更大的工厂的仓库），当然运送产品也是需要费用的，一件产品运送一个单位距离的费用是 11。
假设建立的仓库容量都都是足够大的，可以容下所有的产品。你将得到以下数据：
  • 工厂 ii 距离工厂 11 的距离 xix_i（其中 x1=0x_1=0）。
  • 工厂 ii 目前已有成品数量 pip_i。
  • 在工厂 ii 建立仓库的费用 cic_i。
请你帮助 L 公司寻找一个仓库建设的方案，使得总的费用（建造费用 + 运输费用）最小。
# 分析：
这道题也比较的经典，我们首先考虑对于最后一个仓库如果他里面是有货物的，我们是一定要建仓库的，因为在他后面没有仓库可以让他进行转移，所以必须得建，然后我们就很快的有了一个思路，我们可以设 f[i]f[i] 为在 ii 建仓库，所花费的最小费用，然后我们考虑怎么转移，对于不建仓库的地方，他的所有的货物是一定要转移的，所以我们不妨枚举在 ii 之前的最后一个仓库，那么我们就会有下面的式子
f[i]=min(f[j]+x[i]∑k=j+1ip[k]−∑j+1i(x[k]∗p[k]))f[i] = min(f[j] + x[i] \sum_{k = j + 1}^{i}p[k] - \sum_{j + 1}^{i}(x[k]*p[k]))
然后我们一般对于有 ∑\sum 这种的东西的通用手段就是维护前缀和，我们设 sum[i]sum[i] 为 p[i]p[i] 的前缀和， mul[i]mul[i] 为 x[i]∗p[i]x[i]*p[i] 的前缀和，然后就变成了这样
f[i]=min(f[j]+x[i](sum[i]−sum[j+1])−(mul[i]−mul[j+1]))f[i] = min(f[j] + x[i](sum[i] - sum[j + 1]) - (mul[i] - mul[j + 1]))
我们再考虑什么情况下更优，我们列个不等式然后化简一下就能得到这么一个式子
(f[k1]+sum[k1])−(f[k2]+mul[k2])sum[k1]−sum[k2]<xi\frac{(f[k_1]+sum[k_1]) - (f[k_2]+mul[k_2])}{sum[k_1] - sum[k_2]}<x_i
那么我们就可以设 X(i)=f[i]+mul[i]X(i) = f[i] + mul[i] ， Y(i)=sum[i]Y(i) = sum[i]，然后就可以根据这个去单调队列维护了
#include <cstring>
#include <iostream>
#include <algorithm>
#define int long long
namespace read_write
{
    template <typename T>
    inline void read(T &x)
    {
        x = 0;
        T f = 1;
        char ch = getchar();
        while (ch > '9' || ch < '0')
        {
            if (ch == '-')
                f = -1;
            ch = getchar();
        }
            while (ch >= '0' && ch <= '9')
                x = x * 10 + ch - '0', ch = getchar();
        x *= f;
        return;
    }
    template <typename T>
    inline void write(T x)
    {
        if (x < 0)
        {
            x = -x;
            putchar('-');
        }
        if (x > 9)
            write(x / 10);
        putchar(x % 10 + '0');
    }
    template <typename T>
    T max(T x, T y)
    {
        return x > y ? x : y;
    }
    template <typename T>
    T min(T x, T y)
    {
        return x > y ? y : x;
    }
    template <typename T>
    void swap(T &a, T &b)
    {
        T tem = b;
        b = a;
        a = tem;
    }
}
namespace Solve
{
    using namespace read_write;
    const int N = 2e6 + 10, INF = 0x3f3f3f3f3f3f;
    int n;
    int p[N], c[N], x[N];
    int dp[N], sum[N], mul[N];
    int q[N], hh = 1, tt, pos, ans = INF;
    int calc(int j, int i)
    {
        return dp[j] + x[i] * (sum[i] - sum[j]) - (mul[i] - mul[j]) + c[i];
    }
    int X(int i)
    {
        return dp[i] + mul[i];
    }
    int Y(int i)
    {
        return sum[i];
    }
    long double slope(int k1, int k2)
    {
        return (long double) 1.0 * (X(k1) - X(k2)) / (Y(k1) - Y(k2));
    }
    void solve()
    {
        read(n);
        for(int i = 1 ; i <= n ; ++ i)
        {
            read(x[i]), read(p[i]), read(c[i]);
            sum[i] = sum[i - 1] + p[i];
            mul[i] = mul[i - 1] + p[i] * x[i];
        }
        q[++ tt] = 0;
        for(int i = 1 ; i <= n ; ++ i)
        {
            while(hh < tt && slope(q[hh + 1], q[hh]) < x[i])
                hh ++;
            dp[i] = calc(q[hh], i);
            while(hh < tt && slope(i, q[tt]) < slope(i, q[tt - 1]))
                tt --;
            q[++ tt] = i;
        }
        for(int i = n ; i >= 1 ; -- i)   // 注意！！！！因为可能后面可能有很多仓库里什么都没有，然后你需要特判断一下，否则可能会 100 分但是 unaccepted
        {
            ans = min(ans, dp[i]);
            if(p[i] != 0)
                break;
        }
        write(ans);
    }
}
signed main()
{
    Solve::solve();
    return 0;
}
# To Be Continue……
 
 更新于   阅读次数  次
请我喝[茶]~(￣▽￣)~*
Tokai Teio 微信支付
微信支付
Tokai Teio 支付宝
支付宝
Tokai Teio 贝宝
贝宝