ARC167E One Square in a Triangle 题解

题目传送门

首先对于这道题，一定要读懂题意 /kk，~~比赛的时候因为翻译软件有点抽象导致题意理解错了~~，题干说的是你需要构造的三角形包含且仅包含一个完整的正方形，其实对于 $S$ 为偶数的情况，我们是比较好处理的，难处理的是奇数情况，因为你想要构造一个顶点都在格点上的三角形（先不考虑包含一个完整正方形的情况），偶数的情况我们可以直接以 $2$ 为底，高自然也就出来了，并且一定是能得到一个这个三角形的，那么我们先看看 $S$ 为奇数的时候我们应该怎么先去构造一个面积合法的三角形。

我们知道一个三角形的面积公式是

$S = \lvert \frac{1}{2} \left[ \left(x_2 - x_1\right) \left(y_3-y_1\right) - \left(x_3-x_1\right) \left(y_2-y_1\right) \right] \rvert$

那么我们令其中一个点为 $(0,0)$ ，这是为了方便构造，具体是多少不是特别重要，因为我们可以通过平移来找到等价的三角形，然后这个式子就变成了

$S = \lvert \frac{1}{2} \left( x_2y_3 - x_3y_2 \right) \rvert$

因为我们假定的现在情况为 $S$ 为奇数，那么 $x_2y_3$ 和 $x_3y_2$ 奇偶性不同，既然需要奇偶性不同我们可以直接令 $x_2$ 和 $y_2$ 为最小的两个奇数，同理这也是为了方便构造选其他的应该也能构造出来，尽量不要使得 $x_2 =y_2$ ，因为这样好像有些有解的面积也无法构造出来。然后式子就变成了

$S = \lvert \frac{1}{2} \left( y_3 - 3x_3 \right) \rvert$

这里我们是让 $(x_2,y_2)$ 为 $(1, 3)$ ，那么我为了让剩下的这俩奇偶性仍然不同，最简单的方法即为让 $y = x - 1$ 。那么我们最后的式子就会变成了

$S = \lvert x_3 + \frac{1}{2} \rvert$

那么我们就构造出了一个面积合法的三角形。~~折腾了半天终于构造出来了 QWQ~~

那么现在另外一个问题就来了，我们怎么保证有且只有一个正方形被包含，我们其实打开画图软件玩一下我们按照这个构造出来的图形会发现当 $9 \le x$ ，我们这么构造他就是有且仅有一个正方形

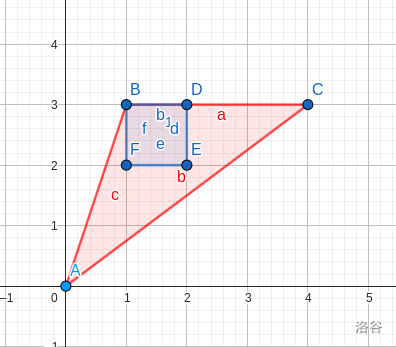
那么这只是一个感性的理解，那么怎么严格证明呢？我们可以将 $AC$ 看成一个斜率为 $k$ 的直线，那么我们想要满足包含那个正方形，就只需要满足 $AC$ 不经过 $E$ ，因为当我们需要的面积越大的时候 $BC$ 是要往上走的，所以只用考虑 $E$ ，那么我们此时要证明的就等价于当 $9\le x$ 直线 $AC$ 的斜率始终小于 $1$ 。那么又因为我们的 $C$ 满足纵坐标永远比横坐标小 $1$ ，那么斜率也就永远小于 $1$ ，所以此结论成立。

那么我们对于奇数的构造方法就差不多结束了。

但是真的结束了吗？我们会发现我们只是讨论了 $9\le x$ 的情况，那小于 $9$ 的奇数咋办？最最最暴力的想法，我们直接手玩不就行了吗 (doge

然后偶数其实同理可以根据奇数的结论去构造，那么如果你看到了这里都能看懂那就祝贺您已经切了一道 $3200+$ 的题，%%%%%

	#include <vector>
	#include <cstring>
	#include <iostream>
	#include <algorithm>

	namespace read_write
	{
	template <typename T>
	inline void read(T& x)
	{
	x = 0;
	T f = 1;
	char ch = getchar();
	while(ch > '9' \|\| ch < '0')
	{
	if(ch == '-')
	f = -1;
	ch = getchar();
	}
	while(ch >= '0' && ch <= '9')
	x = x * 10 + ch - '0', ch = getchar();
	x *= f;
	return;
	}

	template <typename T, typename... Args>
	inline void read(T& first, Args &...args)
	{
	read(first);
	read(args...);
	}

	template <typename T>
	inline void write(T x)
	{
	if(x < 0)
	{
	x = -x;
	putchar('-');
	}
	if(x > 9)
	write(x / 10);
	putchar(x % 10 + '0');
	}

	template <typename T>
	inline T max(T x, T y)
	{
	return x > y ? x : y;
	}

	template <typename T>
	inline T min(T x, T y)
	{
	return x > y ? y : x;
	}

	template <typename T>
	inline void swap(T& a, T& b)
	{
	T tem = b;
	b = a;
	a = tem;
	}
	}

	namespace Solve
	{
	using namespace read_write;

	int t, s;

	void solve()
	{
	read(t);

	while(t -- )
	{
	read(s);
	if(s < 4 \|\| s == 5 \|\| s == 7)
	puts("No");
	else
	{
	if(s==4)
	{
	puts("Yes");
	std :: cout<<"0 0 0 2 2 2" << std :: endl;
	}
	else
	{
	if(!(s & 1))
	{
	puts("Yes");
	std :: cout << "0 0 0 2 " << s / 2 << " " << s / 2 - 1 << std :: endl;
	}
	else
	{
	puts("Yes");
	std :: cout << "0 0 1 3 "<< (s - 1) / 2 << " " << (s - 3) / 2 << std :: endl;
	}
	}
	}
	}
	}
	}

	signed main()
	{
	// freopen("test.in", "r", stdin);
	// freopen("test.out", "w", stdout);

	Solve :: solve();

	return 0;
	}